Evaluating investment performance is not as easy as observing your rate of return. A rate of return is only as meaningful as the methodology used to find it, and the benchmark that it is being compared to. The most common rate of return calculation methodologies are money-weighted rate of return, time-weighed rate of return, and Modified Dietz which is sort of like a hybrid of the two.
The CFA Institute’s guidance on performance calculation methodology explains the preference for time-weighted rate of return as follows:
The GIPS [Global Investment Performance Standards] standards require a time-weighted rate of return because it removes the effects of external cash flows, which are generally client-driven. Therefore, a time-weighted rate of return best reflects the firm’s ability to manage the portfolios according to a specified mandate, objective, or strategy, and is the basis for the comparability of composite returns among firms on a global basis.
As of 2016, all investment dealers are required to calculate and report on the money-weighted rate of return (MWRR) for their clients. MWRR is best used to understand the individual returns of an investor, which are affected by the timing of their cash flows. While useful for estimating individual investor returns, the MWRR is less helpful for appraising portfolio performance against a benchmark. In most cases the timing of your cash flows has little to do with investment decisions and more to do with circumstance. For example, if you receive a large bonus in June and invest it right away, it does not make sense to include the impact of the timing of that cash flow in the performance calculation for the purpose of comparing your portfolio to the index.
Calculating the money-weighted rate of return is an internal rate of return (IRR) exercise, which involves finding the rate of return that sets the present value of all cash flows and the ending value equal to the beginning value. This is relatively easy to do in Excel using the Goal Seek function to solve the following equation.

If we assume that an investor starts with $1m invested in the S&P 500 in March, 2018, and makes one $300,000 contribution at the end of September (day 213 of the 364 day period), to finish with a total of $1.33m at the end of the year, their MWRR would be 3.21% for that year. If instead they had withdrawn $300,000 on day 213, the MWRR increases to 6.58%. The S&P 500 index returned 4.68% over the same time period. Clearly the sensitivity to the timing of cash flows makes this a challenging metric to use for comparison to a market index. If there are no cash flows, the MWRR will produce the same result as the time-weighted rate of return.
The time-weighted rate of return (TWRR) takes a different approach which completely ignores the timing of cash flows. This is the most useful metric if the goal is to compare your portfolio to a benchmark index. The challenge, however, is that the TWRR is not terribly user-friendly. It requires access to the daily value of portfolio assets in order to calculate the rate of return for each sub-period. The sub-period returns are then linked together geometrically to find the portfolio’s rate of return. By linking together rates of return with no regard for the timing of cash flows we get a result that can be easily compared to any asset or index.

In this case we need to know the portfolio value on each contribution date. On the 213th day the S&P 500 portfolio was worth $1.08m (before the $300,000 contribution). This allows us to calculate the first and second sub-period returns.
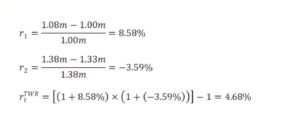
Linking the sub-period returns together, we find the TWRR of 4.68% – the same return as the index despite the cash flow that occurred. If we instead withdraw $300,000, we find the identical result.

This indifference to the timing of cash flows makes the TWRR ideal for benchmarking purposes, but it can also be tedious to collect data for. In our examples we used month-end portfolio values; if a cash flow happens mid-month it can be a challenge to perform the calculation.
Modified Dietz is a performance calculation method that approximates the time-weighted rate of return, recognizing that valuations at the time of each cash flow may not be available. Modified Dietz weights external cash flows by the amount of time they were held in the portfolio. Modified Dietz is still sensitive to the timing of cash flows. At the time of writing, PWL Capital uses Modified Dietz to calculate performance.

Coming back to our example of an S&P 500 portfolio with a single $300,000 cash flow, we can see how Modified Dietz looks relative to TWRR and MWRR. With the single $300,000 cash in flow occurring on day 213, the Modified Dietz return is 3.20%. If we instead make a withdrawal, the Modified Dietz return increases to 6.58%.
From the TWRR sub-period figures we know that sub-period 1 had a positive return while sub-period 2 had a negative return. From this we can observe that both MWRR and Modified Dietz will overstate the return relative to TWRR if a withdrawal is made prior to a period of poor performance, and they will understate the return if a contribution is made prior to a period of poor performance. This detail is extremely important to understanding portfolio returns.
| +$300k on Day 213 | -$300k on Day 213 | No Cash Flows | |
|---|---|---|---|
| Time-weighted | 4.68% | 4.68% | 4.68% |
| Money-Weighted | 3.21% | 6.58% | 4.68% |
| Modified Dietz | 3.20% | 6.58% | 4.68% |
| Contribution Before Negative Performance | Contribution Before Positive Performance | No Cash Flows | |
|---|---|---|---|
| Time-weighted | Unaffected | Unaffected | Unaffected |
| Money-Weighted | Understated | Overstated | Unaffected |
| Modified Dietz | Understated | Overstated | Unaffected |